
modp的类DES算法实现
此为博主在学习密码学课程时编写的作业,有关modp的类DES算法实现。
modpDES算法使用说明
原理简述
1 输入输出参数
key: 64bit的密钥
message:64bit的需要加密的信息,即明文
cipher:64bit的已经被加密过的信息,即密文
2 流程
2.1 轮密钥产生
此处为简单的实现该算法,并充分使用到密钥进行加密与解密过程中,采取
循环右移的方式生成轮密钥,其中每一步都进行 模p 的操作。
2.2 加密函数 f
该算法由于时间和要求的原因,从 DES 的基础上去掉了置换、S-盒替换以及逆置换的操作,仅保留了最其中的 f 函数。为充分进行加密,该算法将会进行16轮相同的加密操作,每轮迭代的过程可以表示如下:
$$
\begin{cases}
L_i = R_{i-1}\
R_i = (L_{i-1} + f(R_{i - 1}, K_i)) % P\
i = 1, 2, 3, …, 16
\end{cases}
$$
其中 f 函数的具体流程如下:
$$
\begin {cases}
R = Inv(R) % P \
R = (R * num + subkey) % P \
\end{cases}
$$
即先对右部求逆,再乘上常数并加上轮密钥,其中每一步都进行了 模p 操作。
求逆部分使用了扩展欧几里得算法,加快了加密的速度。
流程图
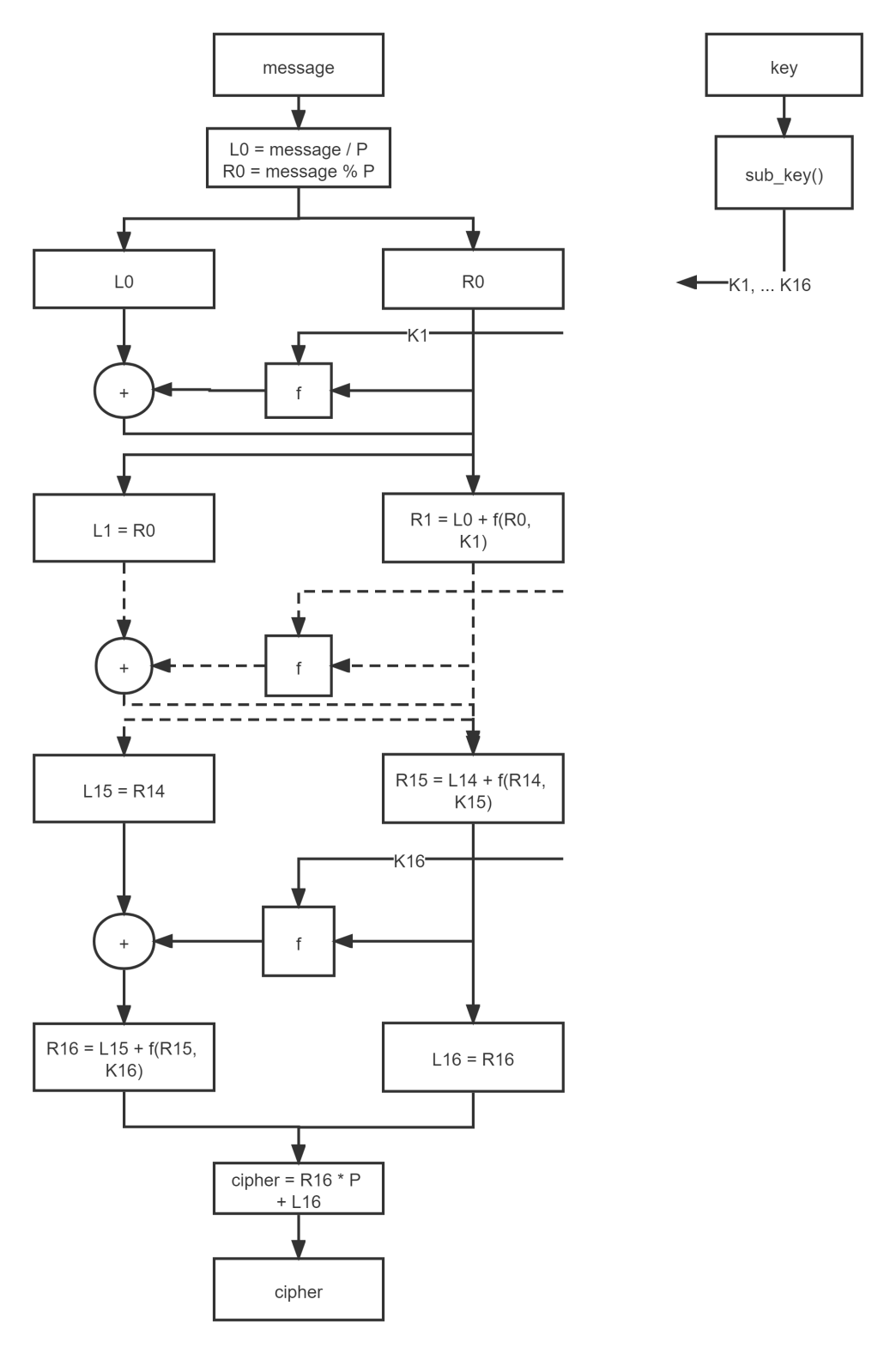
具体实现
此次算法实现较为简单,只编写了4个函数便完成了加密和解密操作:
1 | ll Inv_R(ll num); // 求逆元 |
并定义了一些全局变量方便运算:
1 | const unsigned long P = 49451; // P取值 |
宏定义以及变量类型定义如下:
1 |
|
运行结果
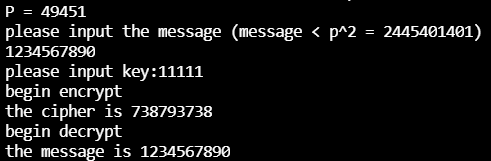
此处预先生成了素数P = 49451,可以看到密文并未超过规定的0~P^2的范围,并且可以完整解密。
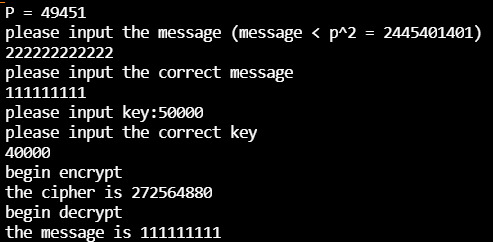
明文和密钥的大小限制是通过输入时进行控制的,处理中并未涉及。
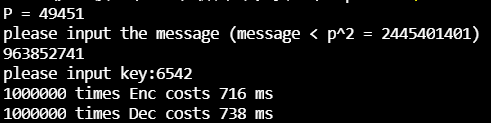
对于明文空间在[0, 2445401401)的数据,进行一百万次加密的平均时间约为720ms, 解密一百万次的平均时间约为735ms。
对于密文空间是否均匀的问题,此处使用P = 257,明文空间为[0, 66049)作为实验样本,收集其中每一个明文对应的密文,绘制成下图:
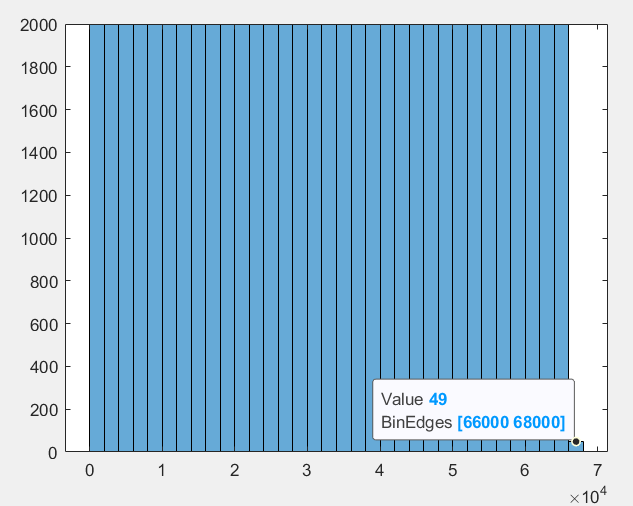
从图中可以发现,密文空间内是均匀分布的,证明该算法的混淆作用良好。
代码实现在博主的GitHub上:https://github.com/hurry-hub/cryptography_work/tree/main/modpDES
