64位RSA算法

2021年12月12日 1k 字大概 4 分钟

此为博主在学习密码学时完成的课堂任务，有关于64位的RSA密码算法。

64位的RSA算法

基本原理

RSA公开密钥密码体制的原理是：根据数论，寻求两个大素数比较简单，而将它们的乘积进行因式分解却极其困难，因此可以将乘积公开作为加密密钥。

基本流程

（1）任意选取两个不同的大素数 p 和 q 计算乘积 n = pq, F_n = (p - 1) (q - 1);

（2）任意选取一个大整数 e，满足 gcd(e, F_n) = 1，整数 e 用做加密钥（注意: e 的选取是很容易的，例如，所有大于p和q的素数可用）

（3）确定的解密密钥 d，满足 (ed) mod F_n = 1，即 ed = k F_n + 1, k ≥ 1是一个任意的整数；所以若知道 e 和 F_n，则很容易计算出 d ；

（4）公开整数 n 和 e ，秘密保存 d ；

（5）将明文m（m < n 是一个整数）加密成密文c，加密算法为

c = E(m) = m ^ e mod n

（6）将密文 c 解密为明文 m ，解密算法为

m = D(c) = c ^ d mod n

然而只根据 n 和 e（注意：不是 p 和 q ）要计算出 d 是不可能的。因此，任何人都可对明文进行加密，但只有授权用户（知道 d）才可对密文解密。

具体实现

由于实现的是64位的RSA算法，则在模时难免会超出unsigned long的最大取值，故需要自行编写大数运算算法进行实现。

1. 大数运算部分

此处定义结构体NUM用以存放将要使用的大整数

typedef struct number{
	int len;
	char symbol;
	int number[LEN];
}NUM, *pNUM;

再编写相应的运算函数，具体如下：

void reverse(int original[], int len);                                // 数组翻转

void print(NUM original);                                             // 打印大数

void number_trim(pNUM original);                                      // 数组翻转

void zero(pNUM original);                                             // 数组清零

int compare_abs(NUM left, NUM right);                                 // 绝对值比较

NUM number(char str[]);                                               // 字符串转大数

NUM anti_add(NUM left, NUM right);                                    // 元加法

NUM anti_add(NUM left, NUM right);                                    // 元减法

NUM add(NUM left, NUM right);                                         // 加法

NUM sub(NUM left, NUM right);                                         // 减法

NUM mul(NUM left, NUM right);                                         // 乘法

void div_with_mod(NUM left, NUM right, pNUM result, pNUM residue);    // 带余数除法

NUM Div(NUM left, NUM right);                                         // 除法

NUM mod(NUM left, NUM right);                                         // 模

2. 素数生成部分

由于RSA算法需要先生成素数 p 和 q 以及 e ，故需要编写素数生成部分，具体如下：

ll gen_rand_num(int len);                                   // 生成大随机数

ll fast_mod(ll a, ll b, ll mod);                            // 计算２的幂

ll fast_pow_mod(ll a, ll b, ll mod);                        // 快速幂

ll mod_mul(ll a, ll b, ll mod);                             // 模乘

ll mod_pow(ll a, ll n, ll mod);                             // 模幂

bool Miller_Rabin(ll n);                                    // Miller-Rabin测试

ll prime(int len);                                          // 生成大素数

3. RSA算法主体

根据之前部分的内容，在已经生成 p 和 q 的基础上计算得出 n = p * q ，然后再根据 ed mod F_n = 1 计算得出 d ，最后再按照加密步骤和解密步骤进行加密、解密，具体如下：

NUM extend(NUM e, NUM F_n, const NUM one);                // 扩展欧几里得求逆，获得解密密钥d

NUM encrypt(NUM e, NUM n, NUM one);                       // RSA加密

void decrypt(NUM d, NUM n, NUM cipher, NUM one);          // RSA解密

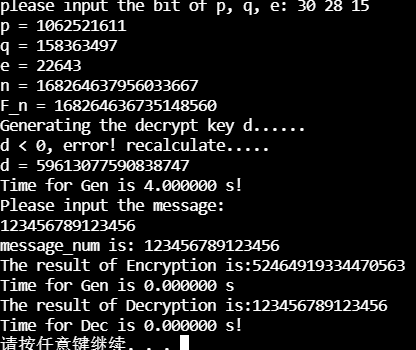
运行截图

该程序用以加密64位以内的十进制整数，可自定义选择 p 、q 以及 e 的长度，并根据对应长度输入明文进行加密，密文为明文加密后对应的十进制数。

从以上结果可以看出，当计算19位的 p 和13位的 q 以及11位的 e 时，计算解密密钥共花费时间3747s，约62min。

由于加密和解密时采用了二进制快速幂的方法，故耗时极短。

经过改进后，求逆部分使用了扩展欧几里得算法，极大的加快了运算速度，同时又用限制条件避免了d为负数的出现。

具体代码放在博主的个人GitHub：https://github.com/hurry-hub/cryptography_work/tree/main/RSA